This is a quite common question that gets asked in interviews to check your understanding of FSM. This is not a straightforward FSM question like the sequence detection one; and if you have not practiced it beforehand, it is easy to get lost. Good news is it extremely easy to understand, and once you have practiced it, it should not take much time to build the FSM.
So, the question generally goes like this: You have a 1-bit input coming in every cycle. The number in any cycle is formed by concatenating the 1-bit input received in the current cycle to the LSB of the previous number. You must drive a 1-bit output which can be either 1 or 0, representing the number formed till that cycle is divisible-by-3 or not respectively.
Let us understand this using an example. Assume the input received in 5 consecutive cycles to be – 1, 0, 1, 1, 0. So the number formed in the respective cycles will be: Cycle 0 – 0 (reset) Cycle 1 – 1 Cycle 2 – 10 Cycle 3 – 101 Cycle 5 – 1011 Cycle 6 – 10110
To solve this, let us assume a variable “x” which will denote the number formed till a particular cycle and is divisible-by-3. Whenever a number is divided by 3, the remainder can assume any of the 3 values: 0, 1 and 2. If remainder is 0, the number is divisible by 3, else the number is not divisible by 3. We will use this concept in making our FSM.
As only 3 remainders are possible, we will have 3 states, namely, REM_0, REM_1 and REM_2. Whenever the current state is REM_0, the output will be 1 depicting the number is divisible-by-3. Now, let us see how we will change states.
At reset, the current state will be REM_0. In the next cycle, we have 2 possibilities: The input can be 0 or 1. The next state will depend on these numbers. Let us see what the remainders will be if we get either of these numbers in the next cycle.
if (in==1’b0), x_next = {x, 0}
{ } is the concatenation operator.
If we convert x_next to decimal, we will get:
x_next = 2*x + 0
As x is divisible-by-3:
next_state = REM_0
Similarly,
if (in==1’b1), x_next = {x, 1}
Converting it to decimal:
x_next = (2*x + 1)
As x is dividible-by-3:next_state = REM_1
Using the same method mentioned above, I have calculated the next states for all possibilities in the picture below ("x_next" denoted by "num"):

Once you have this equation, it will not take you more than 2 minutes to come up with the final FSM as shown below:
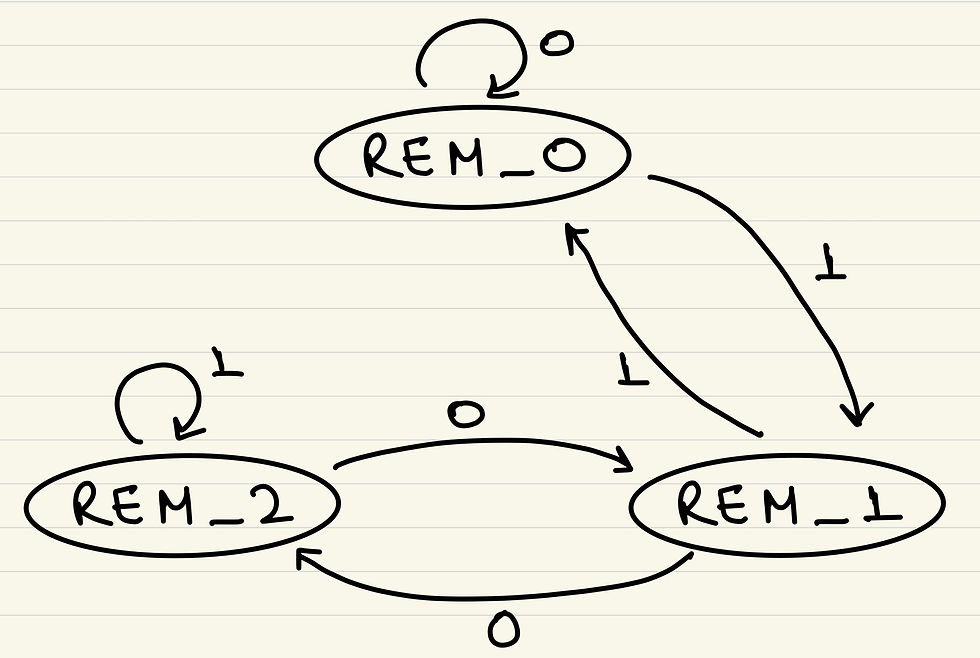
Pretty easy, right?
After understanding this, can you try to make FSM for divisible-by-5? The process is exactly the same and will have 5 states. Give it a try, should not be much hard.
See you in the next article!

Comentarios