RTL code for parameterized Binary to Gray and Gray to Binary conversion

We already know that Gray codes are used extensively in the VLSI industry. In this article, I will present a parameterized Binary to Gray and Gray to Binary converter. The solution presented is very concise and optimized and is good to go to be used in a real design (see source of the article).

Binary to Gray conversion

Let us start with B2G first. Best way to understand the conversion is with an example. I have found that for both G2B and B2G conversion, decimal number 10 is the best example to remind myself of the conversion process if I ever forget. Just memorize the value of 10 in both binary and Gray and write it down in a paper, you will immediately remember the conversion process.

10 in binary is 1010 and 10 in Gray code in 1111. So basically, when converting binary to Gray, starting from MSB, the MSB will be the same, and the consecutive bits are XOR of that bit in binary and the previous bit in binary. See the picture below:

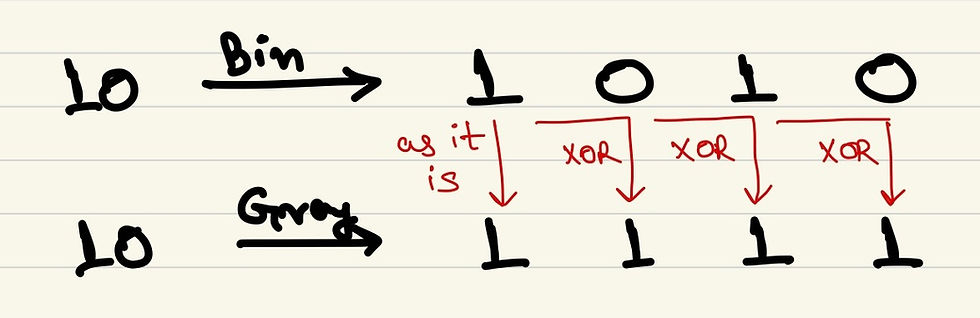
This means that for a 4-bit number: gray[3] = bin[3] gray[2] = bin[3] ^ bin[2] gray[1] = bin[2] ^ bin[1] gray[0] = bin[1] ^ bin[0]

Using the property of XOR that when one of the inputs is 0, XOR gate acts as a buffer, we can re-write gray[3] as: gray[3] = bin[3] ^ 0

gray[2] = bin[3] ^ bin[2]

gray[1] = bin[2] ^ bin[1]

gray[0] = bin[1] ^ bin[0]

Also, if we right shift the binary number by 1, the 3rd bit (MSB) will become zero, 2nd bit will become 3rd bit, 1st bit will become 2nd bit and 0th bit will become 1st bit. See the picture below:

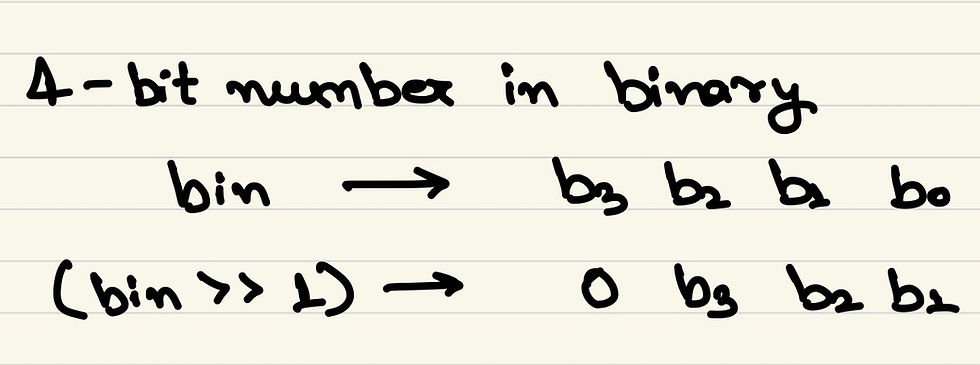
You might have noticed from the picture that if we simply XOR these two numbers, we will get our result. See the example below for our favorite number:

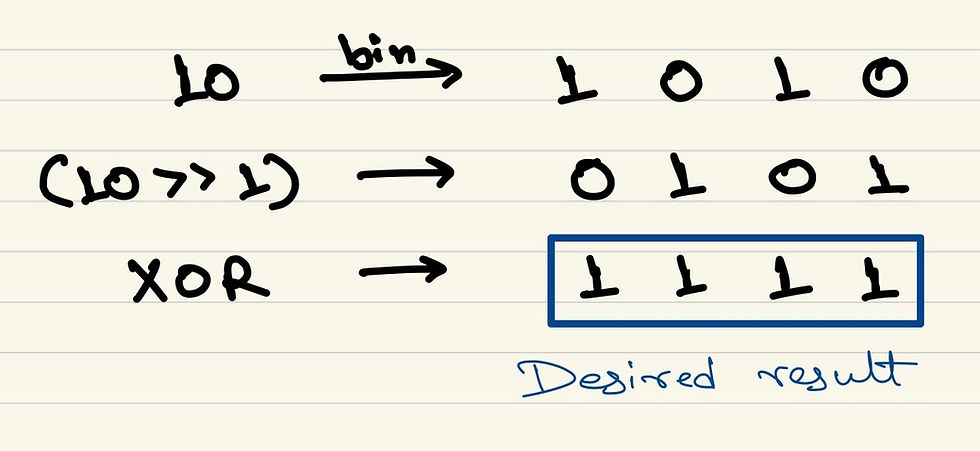
With this knowledge, we can easily write the RTL code as follows:

module b2g #(parameter SIZE = 4)
 (output logic [SIZE-1:0] gray,
 input logic [SIZE-1:0] bin);

 assign gray = (bin>>1) ^ bin;

endmodule

The great thing about this code is, you don’t have to worry about the input width. It is parameterized and will work for any width of input bus.

Gray to Binary conversion

G2B is just a tad bit more complex when compared to B2G. Let us take the example of decimal number 10 again. To get binary number from Gray number, again starting from MSB, the MSB will be the same, but the consecutive bits are XOR of all the previous bits in gray. The picture below should make things clear:

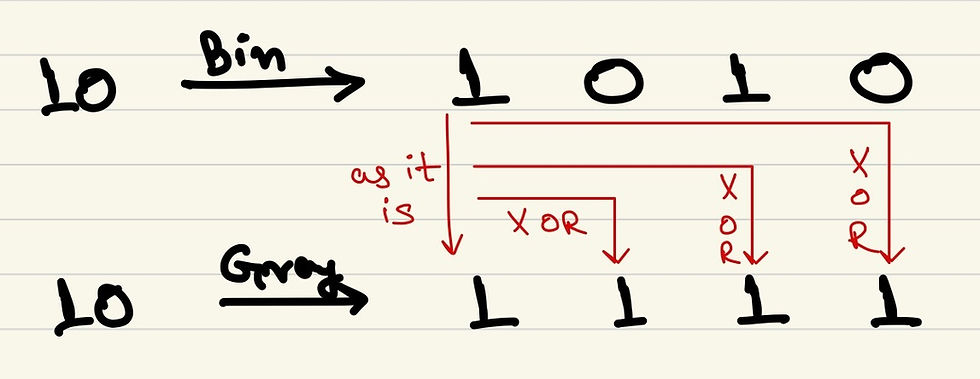
 According to the picture and using property of XOR, we can write: bin[3] = g[3] ^    0   ^    0   ^   0

bin[2] = g[3] ^ g[2] ^    0   ^   0

bin[1] = g[3] ^ g[2] ^ g[1] ^   0

bin[0] = g[3] ^ g[2] ^ g[1] ^ g[0]

The 0th bit of binary is basically the reduction XOR operator applied on all bits of Gray (no shifting involved). Similarly, the 1st binary bit is reduction XOR operator applied on all the bits of Gray but after right shifting it by 1. Therefore, we can deduce that the nth binary bit will be reduction XOR operator applied on all bits of gray after right shifting it by “n.”

Now, we can write the RTL for G2B as follows:

module g2b #(parameter SIZE = 4)
 (output logic [SIZE-1:0] bin,
 input logic [SIZE-1:0] gray);

 always_comb
 for (int i=0; i<SIZE; i++)
 bin[i] = ^(gray>>i);

endmodule

As you can see, we had to use for loop for shifting right the Gray code before reduction operator is applied. This code too will work for any number of input bits without a problem.

See you in the next article!